
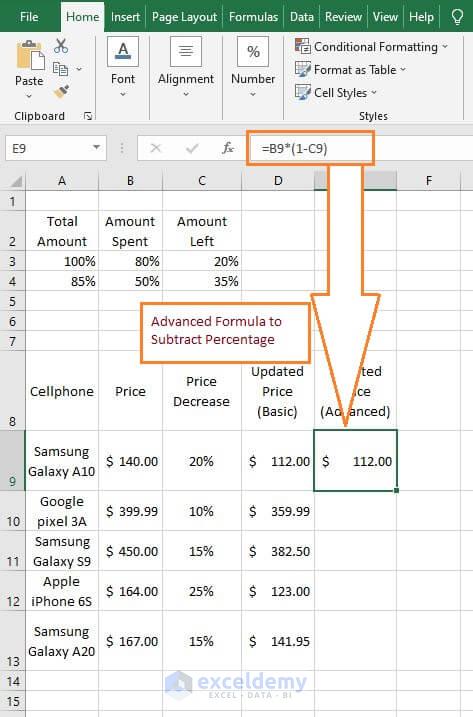
This is because adding 10% is the same as multiplying by $1 + \frac\right)^2\right).$$ 4 Enter the number (minus the percentage sign) and click out of the box for. (That's why if you first get a 10% paycut, and then you get a 10% raise, you are not back where you started). The equation below is one of the more commonly understood definitions of the. Subtracting 10% of that gives you 110-11 = 99, less than what you started with. Say you start with 100 adding 10% gives you 100+10 =110.
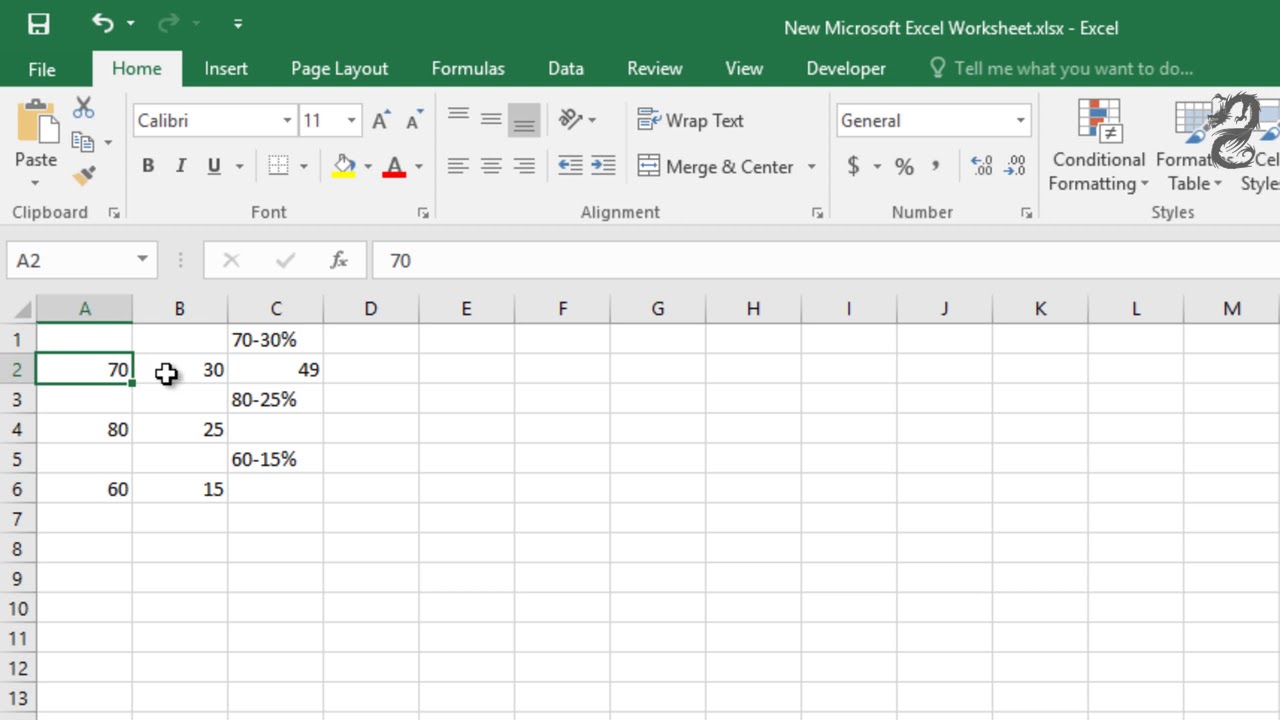
If you first add a percentage, say 10%, and then you subtract 10% of that total, you don't get back to the original amount. Complete the calculation by adding or subtracting as necessary. that you are adding or subtracting percentages of the same quantity. Percentages are like fractions and decimals: they are ways to describe a proportion of a. If you did compound then it is correct that $$100 \times (1 + 0.10) \times (1 + 0.07) = 117.70$$Īnd you would undo it with $$117.70 \div (1 + 0.10) \div (1 + 0.07) = 100$$ To use this method, simply take the number after the of and divide it into the number next to the is. Fluency with addition, subtraction, multiplication and division of whole numbers. The second issue is your lack of compounding the taxes. You seem to understand this in your equation for value. The result of the formula (1+2)3 produces a different result than 1+23. Instead of writing SUM (A1:B1) you can write A1+B1. So a 25% increase must be undone by a 20% decrease. Remember that the basic arithmetic operators (+, -,, /) can be used in formulas using the 'Multiplication and Division before Addition and Subtraction' rule. So to undo the increase (from 400 to 500), instead we should divide as follows:Īnd since $1 \div (1+ 0.25) = (1 - 0.20) $, we would have So it is clear that this multiplication does not work, and we should not expect it to since $(1+ 0.25) \times (1- 0.25) = 0.9375$ not $1$.


 0 kommentar(er)
0 kommentar(er)
